Wiskunde stelling van Pythagoras.wmv YouTube


De Stelling Van Pythagoras In Woorden Uitgelegd

Stelling. De stelling van Pythagoras geeft een verband tussen de lengten van de zijden van een rechthoekige driehoek. Noemt men de lengten van rechthoekszijden, de zijden die aan de hoek van 90° liggen, en , en de lengte van de schuine zijde, de zijde die niet aan de rechte hoek grenst, de hypotenusa, , dan is de bekende wiskundige vorm van de.


De stelling van Pythagoras 5. Een zijde berekenen met Pythagoras YouTube

De stelling van Pythagoras. In een rechthoekige driehoek wordt het verband tussen de lengten a en b van de twee rechthoekszijden en de lengte c van de schuine zijde gegeven door: a 2 + b2 = c2. De zijde c noemen we ook wel de hypotenusa. De stelling van Pythagoras is een belangrijke stelling. Bij tal van berekeningen en bewijzen van andere.


Stelling van Pythagoras YouTube

Wat is de stelling van Pythagoras en wat kan je er mee?In deze video de basis van deze wereldberoemde stelling.Passend bij PythagorasModerne Wiskunde 12e edi.


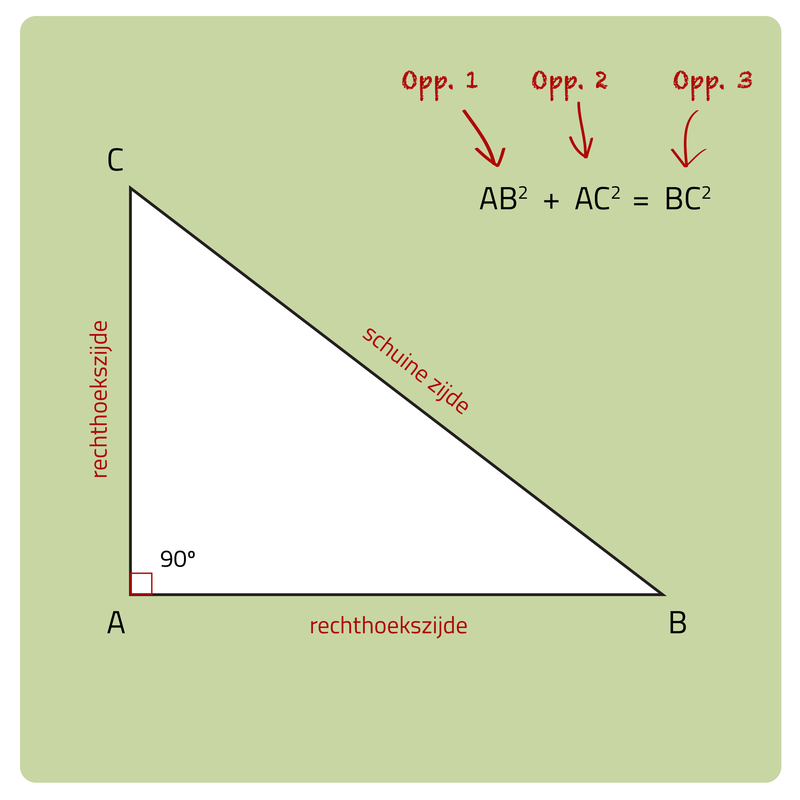
Slimleren Introductie van de Stelling van Pythagoras

De gevreesde stelling van Pythagoras is voor veel studenten een doorn in het oog. Om precies te snappen wat deze stelling inhoudt, overlopen we wat een stelling precies is, hoe we tot de formule van Pythagoras komen, geven we gerichte uitleg en enkele voorbeelden.Met andere woorden: na het lezen van dit artikel weet jij alles van de stelling van Pythagoras, inclusief het toepassen!


Introductie van de stelling van Pythagoras YouTube

Wat is de stelling van Pythagoras, en hoe passen we die formule toe? 📐 Wil je graag meer uitleg over de stelling van Pythagoras? Lees dan onze blog waar je.


Stelling van Pythagoras in Geogebra YouTube

De Stelling van Pythagoras is een formule uit de wiskunde. In rekentaal ziet de stelling van Pythagoras er zo uit: a 2 + b 2 = c 2. Dat spreek je zo uit: a in het kwadraat plus b in het kwadraat is c in het kwadraat. De letters a, b en c staan allemaal voor één van de zijde van een speciale driehoek. a 2, b 2 en c 2 staan voor de lengtes van.


Stelling van Pythagoras voorbeeld 2 YouTube

Onthoudt daarom de stelling van Pythagoras in de algemene vorm: (ene rechthoekszijde)2 + (andere rechthoekszijde)2 = (schuine zijde)2. Of ook wel bekend als: a2 + b2 = c2, waarbij a en b de rechthoekszijden zijn en c de schuine zijde is. Met Slimleren kun je op een leuke manier thuis extra oefenen met de vakken waar jij moeite mee hebt.


Stelling van Pythagoras deel 2 de stelling wiskunde tv YouTube

Wat is de Stelling van Pythagoras? Bron: WiskundeAcademie - (c) Youtube.nl (2024) Vragen na deze uitleg? 26 April, 2024 Bovenstaande video is met zorg gemaakt door de makers van Rekentube.nl. We hopen met deze video dat je meer inzicht hebt gekregen van wat je kunt verwachten bij dit boek. Laat ons weten of de uitleg voor je duidelijk was.


Stelling van Pythagoras Deel 3 Een korte zijde berekenen (2 VMBOK) YouTube

De stelling van Pythagoras kun je alleen gebruiken bij een driehoek waar één hoek in zit van 90 graden. Dit betekent dat de hoek loodrecht is. Met deze formule kun je de zijdes van een driehoek berekenen. De stelling van Pythagoras is a 2 + b 2 = c 2. Als je de lengte van twee zijdes hebt, blijft er dan nog een onbekende die je kunt.


Stelling van Pythagoras voorbeeld 2 YouTube

Videotranscript. In deze video zullen we uitleg geven over de stelling van Pythagoras, wat een zeer leuk onderwerp is. Als je meer en meer wiskunde leert zal je zien dat het een van de pilaren is waarop de wiskunde verderbouwt. Het is nuttig in de meetkunde, het is eigenlijk de ruggengraat van de meetkunde. Je zal het ook kunnen gebruiken om.


uitleg bewijs stelling van Pythagoras YouTube

De stelling van Pythagoras is een van de bekendste wiskunde formules. De stelling luidt: de som van het kwadraat van de lengtes van de rechthoekszijden is gelijk aan het kwadraat van de lengte van de schuine zijde. Kortom: A 2 + B 2 = C 2 Hierbij is A de lengte van de korte zijde, B de lengte van de lange zijde en C de lengte van de schuine zijde.


Wat is de omgekeerde stelling van Pythagoras? (havo/vwo 2) WiskundeAcademie YouTube

Wat betekent de term stelling van Pythagoras? De stelling van Pythagoras is een wiskundige stelling die bedacht is door de Griekse wiskundige Pythagoras. 'Zijn' stelling was alleen niet nieuw voor de wereld, dat komt omdat in Soemer het resultaat al veel langer bekend was. Ook in Babylonië en het oude Egypte werd deze stelling al eerder.


Stelling van Pythagoras II YouTube

Pythagoras (ca. 570-500 v.Chr.) is bij het grote publiek vooral bekend om een beroemde stelling waarmee de lengte van een zijde in een rechthoekige driehoek berekend kan worden (a2+b2 = c2). De kern van deze zogenoemde 'stelling van Pythagoras' was lang daarvoor waarschijnlijk echter al bekend bij de Babyloniërs en Egyptenaren.


Wiskunde stelling van Pythagoras.wmv YouTube

In deze paragraaf wordt de stelling van Pythagoras geïntroduceerd. Allereerst wordt de stelling van Pythagoras gerelateerd aan oppervlakten: De som van de oppervlakten van de vierkanten aan de rechthoekszijden is gelijk aan de oppervlakte van het vierkant aan de schuine zijde. Om dit te verduidelijken laten we een bewijs zien van de stelling.


Stelling van Pythagoras voorbeeld 1 YouTube

De stelling van Pythagoras. Een rechthoekige driehoek heeft 3 zijdes: 2 rechthoekszijden en een schuine zijde. De schuine zijde wordt ook wel eens de langste zijde, of de hypotenusa genoemd. Bij de stelling van Pythagoras kan je de schuine zijde berekenen wanneer je de 2 rechthoekszijden weet. De stelling wordt vaak aangegeven als a 2 + b 2 = c 2.


PPT De stelling van Pythagoras PowerPoint Presentation, free download ID3915661

Wel, dat is een goede vraag. De stelling van Pythagoras is een handig middel voor het vinden van wat je niet weet met behulp van wat je wel weet. Bijvoorbeeld, een rechthoekige driehoek waarvan twee zijden bekend zijn. Eén zijde is onbekend, je weet niet hoe lang deze is. Wel, met behulp van Pythagoras rekenen we dit uit.